Early drug discovery is fraught with failures and frustration, with medicinal chemists frequently returning to the drawing board in search of more promising lead compounds. One way to quickly assess the suitability of a drug is to experimentally determine its log P and log D values, which we will discuss in this article.
The log P and log D of a compound are functional parameters for assessing the bioavailability of a drug. Log P is a ratio of the compound’s solubility in water vs. its solubility in 1-octanol. Log D is calculated similarly but also considers the ionized form of the drug in the water of a certain pH.
Log P and Solubility of Drug Compounds
How to Measure Solubility
When we talk about solubility, we are interested in the maximum concentration of a substance that can dissolve in a solvent.
Solubility depends on the polarity (charge) of the solute and solvent, which together form the solvent system. We can use the dielectric constant of solvents to predict how well a solute will dissolve in it.
However, the best way to assess solubility (or anything, really) is by gathering data experimentally! In these cases, we try to dissolve the solute in two solvents to find a solubility ratio.
We usually use two solvents with opposing properties (one polar, one non-polar) to provide a better comparison—a molecule that is soluble in one will likely be poorly soluble in the other.
The Shake Flask Method
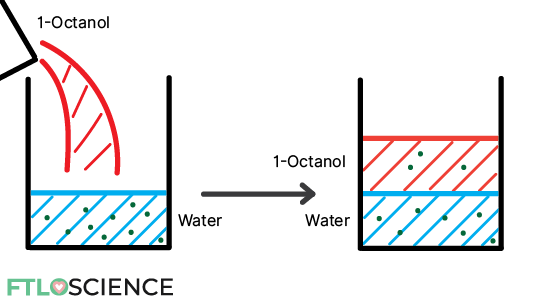
The easiest way to do this is by using the aptly named shake-flask method:
- Gather two solvents of different polarities. For example, water (polar) and 1-octanol (non-polar).
- Dissolve solute of interest in water to a known concentration (e.g., 10 g/L)
- Add the equivalent volume of 1-octanol to the mixture
- Shake for at least 30 minutes!
- Allow the two immiscible layers to separate
- Measure the new concentration in the water layer (e.g., 7 g/L)
- Subtract to find the concentration in the 1-octanol later (e.g., 10 – 7 = 3 g/L)
The Partition Coefficient (P)
Now that we have the concentration of the compound in both 1-octanol and water layers, we can calculate the solubility ratio, also known as the partition coefficient (P):
P=\frac{\text{[Drug]}_{1-octanol}}{\text{[Drug]}_{water}}Since most solutes will heavily favor one solvent over the other, the concentration in each layer will differ by several magnitudes. Therefore, we often use log P values instead, where a difference of 1 unit value corresponds to a 10-fold increase or decrease in the concentration ratio.
Bioavailability and Log P
Bioavailability is the amount of the drug that enters the blood and produces a therapeutic effect, compared to the total administered amount. It is usually expressed as a fraction.
For example, when we swallow a tablet, our stomach hydrolyzes a certain amount. CYP450 enzymes in our liver further metabolize the active ingredient, so the drug’s bioavailability by the time it reaches our bloodstream is far less than 100%.
From a solubility point of view, an oral drug needs to overcome two challenges:
- It needs to be polar to a certain extent (the main component of blood is water)
- It can’t be too polar (non-polar cell membranes control absorption through the gut)
Therefore, an ideal lead compound in drug discovery should have a log P value between 1 and 5. Drugs with a log P greater than 5 are too lipophilic (non-polar), while those with a log P less than 1 are too hydrophilic (polar).
Water and 1-octanol are used as solvents in drug assessment because the former is the main component of blood, while the latter mimics the cell membrane environment.
Improving the Accuracy of Log P using Log D
Log P Problems
While log P is a useful parameter, it fails to account for drugs that ionize in water. Ionization happens when molecules gain or lose a proton, causing them to become positively or negatively charged ions.
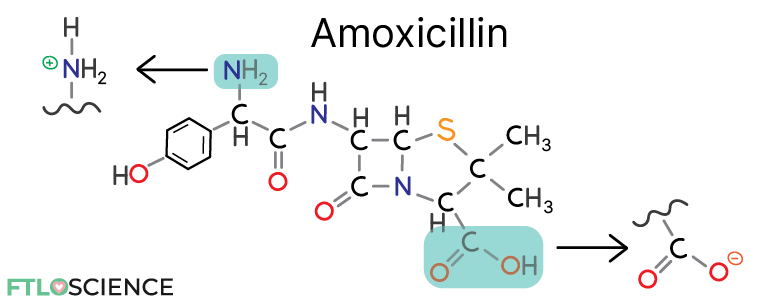
The diagram above shows the chemical structure of amoxicillin, an amphoteric molecule that can act as an acid or a base. Amoxicillin can be ionized by either gaining a proton at the amine group (a base) or losing a proton at the carboxylic acid group (an acid).
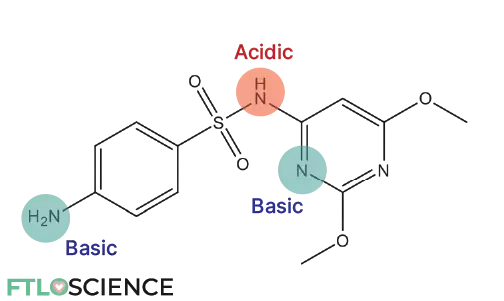
The extent of a drug’s ionization can be calculated based on each functional group’s pKa values:
- If pKa > 7, it will be negatively charged (basic) at pH 7
- If pKa < 7, it will be positively charged (acidic) at pH 7
When we calculate log P, we only measure the initial, unionized drug concentration! This makes any bioavailability assumptions inaccurate, as ionized forms of the drug can still have a therapeutic effect.
Furthermore, if a drug ionizes inside our body, it will become more soluble in water (due to being more polar). This increases its effective concentration in water but erroneously lowers the log P value, since we only calculate the concentration of the drug and not its ionized form!
What is Log D and How Does it Work?
To get around the log P problem, we use a different method to calculate solubility, known as log D (the dissociation coefficient). Log D differs from Log P through an additional term for the ionized form of the drug.
P=\frac{\text{[Drug]}_{1-octanol}}{\text{[Drug]}_{water}}\\[0.1in]
D=\frac{\text{[Drug]}_{1-octanol}}{\text{[Drug]}_{water}+\text{[Ion]}_{water}}
If the drug is acidic, we include the concentration of its ionized form (conjugate base [A–]) in the water phase. We use HA to denote acids:
D_{acid}=\frac{\left[ HA_{1-octanol} \right]}{\left[ HA_{water} \right]+\left[ A^{-}_{water} \right]}If the drug is basic, we include the concentration of its ionized form (conjugate acid [BH+]) in the water phase:
D_{base}=\frac{\left[ B_{1-octanol} \right]}{\left[ B_{water} \right]+\left[ BH^{+}_{water} \right]}Log D values provide us with more accurate predictions for ionizable compounds.
Log D is a pH-Dependent Term
While log P values are pH-independent (they don’t change with pH), log D values represent the solubility of a drug at a specific pH. This is because the extent of ionization (and hence, the concentration of ions) changes with pH.
For pharmaceutical calculations, we usually use physiological (blood) pH of 7.4 to assess bioavailability, although other environments of interest include the stomach (pH 1.5 to 3.5) and the intestine (pH 6 to pH 7.4). These different environments are especially important for studying extended-release or enteric-coated formulations.
The graph below shows the antimicrobial drug sulfadimethoxine’s solubility (log S) vs. pH. It is least soluble at around pH 4, which corresponds to its unionized form.

- As the pH goes below 4 (more acidic solution), the basic nitrogen atoms are protonated, forming a positively charged ion. This increases the solubility of the drug.
- As the pH goes above 4 (more basic solution), the acidic nitrogen atom is deprotonated, forming a negatively charged ion. This also increases the solubility of the drug.
Comparing the Predictive Accuracy of Log P and Log D
Experimental data from a study in 2007 showed that log D values gave more accurate predictions than log P values. The study compared both values with actual bioavailability data from real drug libraries used by researchers, showing that inflated log P values could lead to viable drug compounds being wrongly discarded in early drug discovery (false negatives).
These false negatives accounted for 0.6% to 2.3% of the total drug libraries screened, or 600 to 2,300 additional lead compounds for every 100,000. This small but significant increase widens the pool of potential drugs that would have otherwise been discarded in the initial lead identification stage.
Since 95% of all drugs on the market are ionizable (75% basic, 20% acidic, 5% neutral) at physiological pH, it makes sense that we use log D instead of log P values to assess the potential suitability of lead compounds for further development.
About the Author

Sean is a consultant for clients in the pharmaceutical industry and is an associate lecturer at La Trobe University, where unfortunate undergrads are subject to his ramblings on chemistry and pharmacology.




