How to Calculate the Rate Constant for Two-Compartment Model Drugs

When drugs enter our bodies, we can trace their behavior as they are absorbed into our bloodstream before being metabolized and removed. Most drugs follow linear processes (zero order, first order, second order, etc.) consistent with a one-compartment model. However, some drugs follow two-compartment models, which makes pharmacokinetic calculations like finding the rate constant more complicated.

The residual line method can be used to calculate the rate constant for two-compartment models, where the distribution and elimination phases are treated as two separate equations.

Drugs and Pharmacokinetic Models

One vs. Two Compartment Models

Pharmacokinetics is the study of how the body responds to a drug. Typically, drugs are absorbed into our circulatory system (oral dosage forms, inhalation, patches) or are directly administered (intravenous drips/injections).

Once the drug is in our blood, it is transported to the site of action where it can exert its therapeutic effect. Of course, they don’t stay within our blood forever! Enzymes in our liver metabolize these chemicals, while our kidneys help to eliminate them from our circulatory system.

A typical concentration vs. time profile of a drug is seen below:

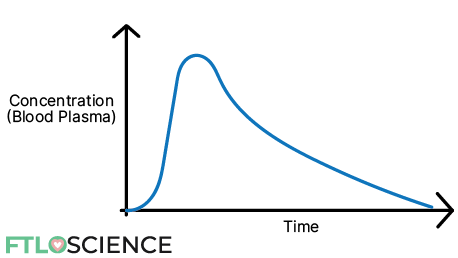
There is a sharp increase in concentration initially, followed by a slower drop-off. Suppose we want to look specifically at the metabolism and elimination of the drug. In that case, we can plot a natural log of concentration vs. time curve from the maximum concentration to the lowest concentration:

The straight line tells us that this is a 1^st order elimination that follows a one-compartment model, with an elimination rate constant (k) given by the gradient. If you are unfamiliar with basic pharmacokinetics, you can visit this guide, which explains elimination kinetics in greater detail.

In drugs that follow two-compartment models, the same ln Cp vs. time plot produces two distinct ‘phases’.

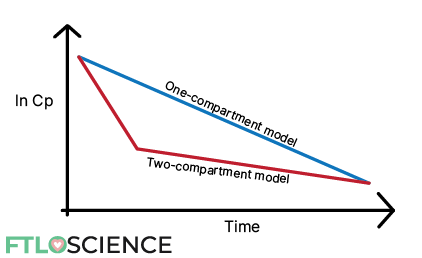
In the following sections, we discuss why drugs might exhibit this behavior and how we can calculate the rate constant for two-compartment models.

Why Two Compartments?

When we gather drug concentration data from a patient, we take blood samples and measure the concentration of the drug within those samples (usually in the range of μg/ml). We then plot this concentration over time to determine the pharmacokinetics of the drug molecule.

In a one-compartment model, we assume that all the drug molecules in a patient are confined to their blood. This assumption means that any decrease in drug concentration implies the drug is being metabolized or eliminated.

Of course, the reality isn’t as simple as that. Drug molecules can diffuse into tissues, fats and organs and attach themselves to proteins.

While most drugs can be modeled reasonably accurately using a one-compartment model, drugs that are more prone to compartmentalization include:

• Lipophilic (hydrophobic) molecules (e.g., statins, alpha/beta-blockers)
• Large molecules (e.g., digoxin)
• Molecules with high affinity to proteins (e.g., thyroxine, diazepam)

In these cases, plotting ln Cp vs. time shows a distribution phase followed by a distinctly separate elimination phase:

After administration and maximum concentration is reached, the drug undergoes the distribution phase. In this phase, there is a net flow of drug molecules from the circulatory system into tissues and organs.

During the distribution phase, the drug concentration in the blood decreases rapidly because both distribution and elimination occur (see diagram below).

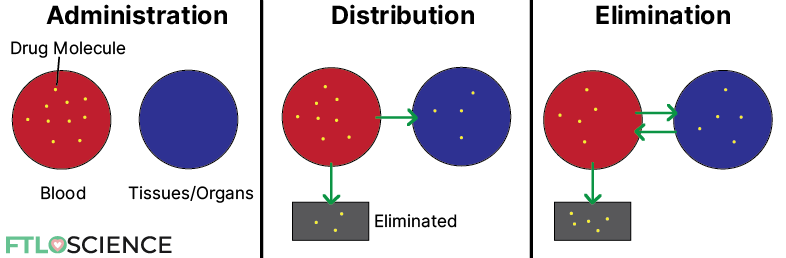
After some time, an equilibrium is established between the blood and surrounding compartments. At this point, any changes in drug concentration in the blood are due to elimination. Hence it is known as the elimination phase.

Calculating Rate Constant for Two-Compartment Models

The Residual Line Method

Since two distinct slopes exist in two-compartment models, we cannot perform the same one-compartment calculations to find the elimination rate constant for such drugs. We need to find the distribution rate constant and elimination rate constant separately!

Remember:

• Distribution phase: both distribution and elimination
• Elimination phase: only elimination

We, therefore, need to subtract the elimination contribution in the distribution phase to find the distribution data. How do we do this? We can back-extrapolate the elimination phase!

We back-extrapolate the elimination data (the last few data points) back to the initial time to get an elimination line of best fit (the red dotted line in the graph below).

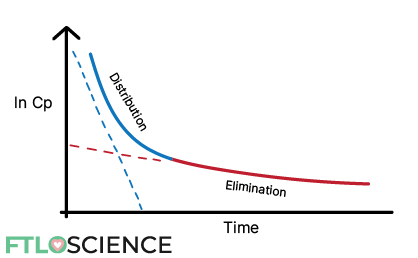
We can subtract the newly extrapolated elimination data from the distribution data (the first few data points) to get a distribution line of best fit (blue dotted line). Since it has been subtracted from the actual values, we call this a residual line.

Rate Constants: k₁₂, k₂₁, k

Now that we have two straight lines to work with, we can extract two critical values from the equation of the line (y = mx + c): the slope (m) and the y-intercept (c).

Graphing software like excel can help you quickly find the equation of a straight line from datasets.

From the distribution data:

The slope = α
The y-intercept = ln Cp₀ (ln Cp at time = 0)
Maximum concentration A = e^{ln Cp0}

From the elimination data:

The slope = β
The y-intercept = ln Cp₀
Maximum concentration B = e^{ln Cp0}

Using this data, we can find three separate rate constants.

The rate constant for drug movement from first to second compartment (blood to tissues):

k_{12}=\frac{AB(\beta-\alpha)^{2}}{(A+B)(A\beta+B\alpha)}

The rate constant for drug movement from second to first compartment (tissues to blood):

k_{21}=\frac{A\beta+B\alpha}{A+B}

The elimination rate constant (blood to elimination):

k=\alpha\beta\frac{A+B}{A\beta+B\alpha}=\frac{\alpha\beta}{k_{21}}