What’s in a wavelength? In chemistry and physics, we come across this parameter in a range of calculations, often to do with photons and light. In this concise guide, we’ll cover all you need to know about the relationship between wavelength, frequency and energy in the context of photons and the electromagnetic spectrum.
Same Speed, Different Wavelengths and Frequencies
Light is delivered in massless packets known as photons. Being massless, photons always travel at maximum speed—the speed of light (c)—but possess different wavelengths. Since they are small enough to be considered quantum particles, photons can exist as waves, with a wavelength (λ) corresponding to the distance between each repeating point in the wave.
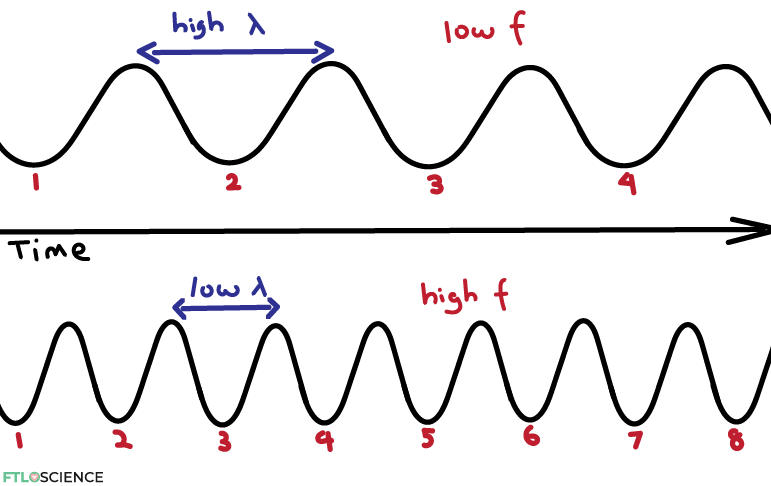
Frequency (f) is a measure of how ‘frequently’ a wave appears within a period of time. As can be seen in the diagram above, as wavelength decreases (the waves become closer together), frequency increases (more waves in the same time frame).
The relationship between energy (E), frequency and wavelength can be described with this equation:
E=hf=\frac{hc}{\lambda}| Symbol | Parameter | Constant Value/SI Units |
|---|---|---|
| E | Energy | Joules (J) |
| h | Planck constant | 6.626 x 10-34 Joules seconds (J s) |
| f | Frequency | Hertz (Hz) or seconds-1 (s-1) |
| c | Speed of light | 2.998 x 108 meters per second (m/s) |
| λ | Wavelength | Meters (m) |
The energy is simply the photon’s frequency multiplied by the Planck constant (h). Frequency and wavelength are inverse correlated by way of the speed of light (c):
f=\frac{c}{\lambda}\\[0.1in]
c=f\lambda The Electromagnetic Spectrum
Light emitted from the Sun is the product of black body radiation from the intense heat generated by nuclear fusion processes within its core (in-depth reference from Uppsala University can be found here). This, in turn, produces photons that have a range of wavelengths from about 10-7 m to 10-6 m, with a peak somewhere in between. On the electromagnetic spectrum, this corresponds to the range of visible light, along with some overlap with the infrared and ultraviolet regions. Our ability to see in the visible range isn’t a coincidence, but a result of evolution taking advantage of the abundance of photons with these wavelengths reaching Earth.

The electromagnetic spectrum shown above shows us the types of radiation associated with each wavelength/frequency. Radio waves have the largest wavelength (smallest frequency, smallest energy) while X-rays and gamma rays have the smallest wavelength (largest frequency, largest energy). You can use the equation mentioned above to calculate the energy associated with each photon of a specific wavelength. For example, for a photon with a wavelength of 10-7 m corresponding to ultraviolet radiation:
E=\frac{hc}{\lambda}\\[0.1in]
=\frac{ \left( 6.626\: \ast\:10^{-34}\:J\:s \right)\times\left( 2.998\:\ast\:10^{8}\:m\:s^{-1} \right)}{10^{-7}\:m} \\[0.1in]
=1.986\times10^{-18}\:J
Each photon of this wavelength has an energy of 1.986 x 10-18 joules, so be sure to put on your sunscreen to avoid skin damage from the barrage of these ultraviolet photons!
The equation can be rewritten to calculate wavelength (and frequency), speed of light and Plank constant.
\lambda=\frac{hc}{E}\\[0.1in]
c=\frac{\lambda E}{h}\\[0.1in]
h=\frac{\lambda E}{c}\\[0.1in]
About the Author

Sean is a consultant for clients in the pharmaceutical industry and is an associate lecturer at La Trobe University, where unfortunate undergrads are subject to his ramblings on chemistry and pharmacology.